додаток 1. Методи
розв’язування найпростіших диференційних рівнянь
Рівняння вигляду
|
|
(Д1.1) |
,де 
- незалежна змінна, 
- шукана функція,
називається диференційним рівнянням порядку 
.
Функція 
є розв’язком рівняння (Д1.1) на відрізку 
, якщо
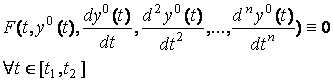
Рівняння першого порядку
іноді можна
записати в явній формі:
|
|
(Д1.2) |
.Якщо, крім
рівняння (Д1.2), ще відома умова
|
|
(Д1.3) |
,тоді задача
відшукання є задачею Коші.
Теорема Пікара Нехай права частина диференційного рівняння (Д1.2)
визначена в області 
і є неперервною в цій
області, а тому обмеженою
.
Часткові похідні функції також обмежені на 
:
.
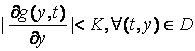Тоді існує єдиний розв’язок задачі Коші
(Д1.2), (Д1.3) на відрізку .
Як знайти
розв’язок Задачі Коші? Розглянемо декілька найпростіших випадків.
1)
рівняння з розділеними змінними
має вигляд:
Його можна
переписати наступним чином
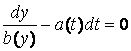
чи
,
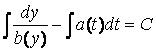де С – деяка
константа.
Приклад Д1.1
Знайдемо
розв’язок задачі Коші
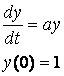
Тут 
. Тоді
.
Підставляємо
початкову умову
.
Тоді
розв’язок має вигляд 
Приклад Д1.2
Знайдемо
розв’язок рівняння
Тут 
. Тоді
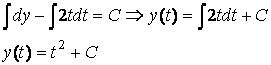
2)
Лінійне диференційне рівняння має
вигляд:
Якщо 
, рівняння називається однорідним.
Однорідне
рівняння є рівнянням з розділеними змінними:
,-
і має
розв’язок:
.
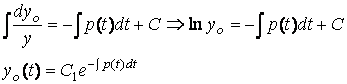Розв’язок
лінійного неоднорідного рівняння можна представити у вигляді:
,
де
- розв’язок
однорідного рівняння,
- один частинний
розв’язок лінійного неоднорідного рівняння. Його знаходження є окремим ділом
кожної задачі.
Приклад Д1.3
Розв’язати
диференційне рівняння:
.
Розв’язок
однорідного рівняння має вигляд:
.
Частковий
розв’язок будемо шукати серед функцій – констант:
.
Підставляючи
її в диференційне рівняння, отримаємо
,
звідки
.
Загальний
розв’язок має вигляд:
3)
Системи лінійних диференційних
рівнянь:
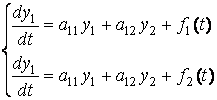
при 
, така система називається однорідною системою:
.
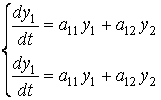Спочатку
слід знайти 
- розв’язки
характеристичного рівняння системи:
,
де 
- матриця коефіцієнтів
моделі, 
- одинична матриця.
Якщо 
, розв’язок однорідної системи шукається у вигляді:
,
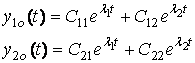Якщо 
, тоді у вигляді:
,
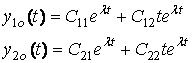Розв’язок
системи лінійних неоднорідних рівнянь є сума
,
де
- розв’язок однорідної
системи рівняння,
- один частинний
розв’язок лінійної неоднорідної системи рівнянь.
Приклад Д1.4
Розв’язати
систему однорідних диференційних рівнянь:
Складемо
рівняння:
,
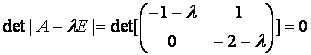звідки
.
Розв’язком
цього рівняння є 
.
Отже,
розв’язок системи набуває вигляду:
.
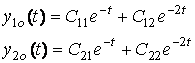Додаток 2. Можливості використання
табличного процесора Excel в дослідженні економічних систем
Табличний процесор Excel входить
до складу програм Microsoft Office. Завантажити процесор можна за допомогою клавіші “ПУСК” (“START”)
робочого стола Windows; його можна знайти серед Програм Microsoft Office.
Робоче вікно Excel складається з
комірок, які мають адреси, що складаються з літери стовпчика і номеру рядка.
Наприклад, A3. В кожний момент часу одна комірка є активною. На ній стоїть курсор
управління. Переведення курсору (зміна активної комірки) можлива за допомогою клавіатури, або “мишки”.
В комірку Excel можна вводити
різноманітну інформацію різного формату. Виділяють три різновиди цієї
інформації:
1)
числа, текст, дати, тощо;
2)
формули обчислень;
3)
функції.
Формули Excel починаються зі знаку
“=” і містять числа, знаки математичних операцій і адреси комірок, в яких
записана числова інформація. Наприклад,
.
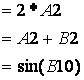Формули, як і іншу інформацію, можна
копіювати з однієї комірки в іншу за допомогою стандартної процедури копіювання
Windjws. При цьому адреси комірок в формулах змінюються відповідно зміни
комірки вставки нової формули.
Частина адреси формули (літера
стовпчика чи номер рядка) може не змінюватися при копіюванні формули, якщо
перед ній стоїть знак “$”. Така адреса називається абсолютною. Наприклад, 
.
Функції Excel працюють з однією
коміркою чи з блоком комірок. Блок комірок складається з прямокутної області
робочого листа Excel. Адреса блоку складається з адреси лівої верхньої комірки, двокрапки і
адреси нижньої правої комірки. Наприклад:
Вбудовані функції можна ввести за
допомогою команд меню Вставка-Функція чи за допомогою спеціальної іконки над
робочим листом.
Наприклад, функція суми чисел, які
знаходяться в блоці комірок
.
Таблиця Д3.1
Функції Excel, які можуть бути
корисними в економічних дослідженнях:
|
Функція |
Дія |
|
=СЛЧИС() |
Генерація випадкового числа,
рівномірно розподіленого на [0,1]. Для імітації економічних подій (прихід
клієнтів) |
|
=ЕСЛИ(D;A;B) |
Якщо логічна умова D є правдою,
тоді виводиться значення операції A. Інакше виводиться значення операції B. Наприклад,
обчислення модуля числа, записаного в
комірці A1: =ЕСЛИ(A1>0;A1;-A1) |
|
=ЛИНЕЙН(блок Y; блок X; константа;
статистика) |
Обчислює рівняння регресії |
|
=ПЗ (ставка; число періодів;
виплата) |
Оцінює інвестиційну привабливість.
Наприклад, ПЗ(4,5%;5;1000)=-4389,98 Каже про те, що можна вкласти 4000
(бо менше значення функції) на 5 періодів (років), якщо кожен рік обіцяють
повертати 1000, а банківська ставка 4,5% |
|
=ППЛАТ (ставка; число періодів;
поточна виплата) |
Обчислює кількість для погашення
суди. Наприклад, ми хочемо взяти суду на
10000 під закладну 8% на рік (8/12=0,67%) строком на 25 років (25*12=300
місяців) ППЛАТ(0,67;300;100000)=-774,47 каже про те, що слід кожного місяця
виплачувати 7774,47 для погашення. |
|
=НОРМА(число періодів; виплата;
вкладання) |
Обчислює швидкість обороту НОРМА(5;1000;--3000)=20% Вкладення 3000 гарантує за 5 років
виплату по 1000 при обороті 20% |
|
=АМР(вартість; залишок; період) |
Амортизація =АМР(8000;500;10)=750 обчислює амортизацію за кожен рік |
. Після запису функції в рядку формул слід виділити блок
комірок, де буде результат, і натиснути комбінацію клавіш Додаток 2. основи програмування в редакторі Visual Basic for Applications
(VBA) в середовищі Excel.
VBA – відносно легка мова програмування. В середовищі Excel вона дозволяє створювати свої власті функції (function) і підпрограми
(Sub), які потім використовуються користувачем в роботі з інформацією на
листах. Крім того, VBA використовує технологію візуального програмування, тобто створення
робочої поверхні виконання програми та елементів управління безпосередньо на
екрані.
Завантаження редактора VBA виконується
за наступною схемою:
Сервіс à макрос à Редактор Visual Basic.
Тексти власних функцій і підпрограм
записуються в лист модуля, який потрібно створити, користуючись оператором меню
“вставка – модуль”.
Основне тіло функції має вигляд:
Function <Fname> (<список параметрів через кому>)
<текст функції>
<Fname>=<значення,
яке має вертати функція>
End Function
Тіло підпрограми:
Sub <Fname> (<список параметрів через кому>)
<текст функції>
<Fname>=<значення,
яке має вертати функція>
End Sub
Функції і підпрограми можуть йти одна
за одній в модулі.
ПРИКЛАД Д3.1
Функція VBA, що повертає квадрат
числа, яке вводиться як параметр.
Function
Kvadrat(A)
Dim
B As Single
B =
A*A
Kvadrat
=B
End
Function
Використання цієї функції може мати
вигляд:
=Kvadrat (A2)
Тоді вона виведе в поточній комірці
листа Excel значення квадрату числа, яке записано в комірці за адресою A2.
Основні типи змінних в VBA.
Опис змінних, які використовуються в
функції, має наступний вигляд:
Dim <змінна> As <тип>.
Таблиця Д3.1 Основні типи даних VBA
|
Тип |
Опис |
|
Ціле число |
Integer |
|
Число з плавуючою точкою |
Single |
|
Дійсне число подвійної точності |
Double |
|
Логічний тип |
Boolean |
|
Тип дати |
Date |
|
Рядок тексту |
String |
|
Будь-яке значення |
Variant |
|
Масив (вектор чи матриця) |
Dim
A(4) As Single |
Таблиця Д3.2 Основні операції над
даними в VBA
|
Операція |
Формат
(приклад) |
|
Присвоювання |
F=3.5 G=2*F |
|
Умовний оператор |
IF
X>0 then A=X-4 Else A=0 EndIf |
|
Оператор циклу |
For
I=0 to 10 A(i)=2+I End
Do |
|
Звертання до значення комірки
поточного листа з певною адресою |
Range(“A2”). Value |
|
Звертання до комірки по місцю на
листі |
Cells(I,J) |
Таблиця Д3.2 Основні функції в VBA
|
Функція |
Формат
(приклад) |
|
Модуль
числа А |
B=Abs(A) |
|
Косинус числа А |
B=Cos(A) |
|
Експонента числа А |
B=Exp(A) |
|
Натуральний логарифм |
B=log(A) |
|
Випадкове число, рівномірно
розподілене на [0,1] |
Randomize B=Rnd |
|
Квадратний корень з числа |
B=Sqr(A) |
|
Ціла частина числа |
B=Int(A) |
Додаток 3. Статистичні
таблиці
1.
Нормальний розподіл
Нормальний розподіл величини 
визначається наступною
функцією розподілу:
,
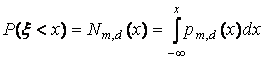де 
- ймовірність того, що
величина 
, 
- густина розподілу з
середнім 
і
середньо-квадратичним відхиленням 
:
.
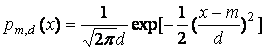Функція Лапласа, представлена в таблиці Д3.1,
має визначення 
, а густина розподілу 
.
За цим значенням можна легко найти функцію 
:
Таблиця Д3.1. Значення функції Лапласа Ф(x)
|
|
|
|
|
|
|
|
0 |
0,398948 |
0 |
1,05 |
0,229886 |
0,848869 |
|
0,05 |
0,39845 |
0,519922 |
1,1 |
0,217855 |
0,859762 |
|
0,1 |
0,396958 |
0,53977 |
1,15 |
0,205939 |
0,870059 |
|
0,15 |
0,394485 |
0,559495 |
1,2 |
0,194189 |
0,879768 |
|
0,2 |
0,391048 |
0,579047 |
1,25 |
0,182652 |
0,888901 |
|
0,25 |
0,386674 |
0,598381 |
1,3 |
0,171371 |
0,89747 |
|
0,3 |
0,381393 |
0,61745 |
1,35 |
0,160386 |
0,905489 |
|
0,35 |
0,375246 |
0,636213 |
1,4 |
0,14973 |
0,912975 |
|
0,4 |
0,368276 |
0,654627 |
1,45 |
0,139433 |
0,919947 |
|
0,45 |
0,360532 |
0,672653 |
1,5 |
0,12952 |
0,926423 |
|
0,5 |
0,352071 |
0,690257 |
1,55 |
0,120011 |
0,932424 |
|
0,55 |
0,342949 |
0,707404 |
1,6 |
0,110922 |
0,93797 |
|
0,6 |
0,33323 |
0,724066 |
1,65 |
0,102266 |
0,943083 |
|
0,65 |
0,322977 |
0,740214 |
1,7 |
0,09405 |
0,947786 |
|
0,7 |
0,312259 |
0,755827 |
1,75 |
0,086279 |
0,952099 |
|
0,75 |
0,301142 |
0,770884 |
1,8 |
0,078951 |
0,956047 |
|
0,8 |
0,289696 |
0,785369 |
1,85 |
0,072066 |
0,95965 |
|
0,85 |
0,277989 |
0,799269 |
1,9 |
0,065617 |
0,962931 |
|
0,9 |
0,266089 |
0,812573 |
1,95 |
0,059596 |
0,965911 |
|
0,95 |
0,254063 |
0,825276 |
2 |
0,053992 |
0,968611 |
|
1 |
0,241974 |
0,837375 |
2,05 |
0,048793 |
0,97105 |
Якщо 
, тоді значення функції Лапласа можна знайти за формулою:
.
2.
t-розподіл Стьюдента
Якщо 
- нормально
розподілені незалежні випадкові величини, а 
- випадкова величина, яка від них залежить, тоді випадкова
величина:
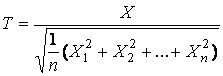
має t-розподіл Стьюдента.
,
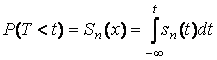де 
- ймовірність того, що
величина 
, 
- густина розподілу.
Функція розподілу, представлена в таблиці
Д3.2, має визначення:
.
Таблиця Д3.2. Значення функції Т
|
|
0,01 |
0,05 |
0,9 |
|
1 |
63,65 |
12,70 |
6,31 |
|
2 |
9,925 |
4,303 |
2,92 |
|
3 |
5,841 |
3,182 |
2,353 |
|
4 |
4,604 |
2,776 |
2,132 |
|
5 |
4,032 |
2,571 |
2,015 |
|
6 |
3,707 |
2,447 |
1,943 |
|
7 |
3,499 |
2,365 |
1,895 |
|
8 |
3,355 |
2,306 |
1,86 |
|
9 |
3,25 |
2,262 |
1,833 |
|
10 |
3,169 |
2,228 |
1,812 |
|
11 |
3,106 |
2,201 |
1,796 |
|
12 |
3,055 |
2,179 |
1,782 |
|
13 |
3,012 |
2,16 |
1,771 |
|
14 |
2,977 |
2,145 |
1,761 |
|
15 |
2,947 |
2,131 |
1,753 |
|
16 |
2,921 |
2,12 |
1,749 |
|
17 |
2,898 |
2,11 |
1,74 |
|
20 |
2,845 |
2,086 |
1,725 |
|
25 |
2,787 |
2,060 |
1,708 |
|
30 |
2,75 |
2,042 |
1,697 |
|
40 |
2,704 |
2,021 |
1,684 |
3.
F-розподіл Фішера
Якщо 
, 
- нормально
розподілені незалежні між собою сукупності випадкових величин, серед них є n та m незалежних величин відповідно. Тоді
випадкова величина:
,-
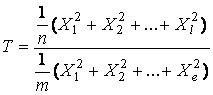має F-розподіл Фішера:
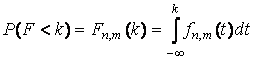, де 
- густина розподілу.
Функція розподілу, представлена в таблиці
Д3.3, має визначення:
.
Таблиця Д3.2. Значення функції Т
А) для 
|
|
1 |
2 |
3 |
4 |
10 |
20 |
|
1 |
161 |
200 |
216 |
225 |
242 |
248 |
|
2 |
18,51 |
19 |
19,16 |
19,25 |
19,3 |
19,44 |
|
3 |
10,13 |
9,55 |
9,28 |
9,12 |
8,79 |
8,66 |
|
4 |
7,71 |
6,94 |
6,59 |
6,39 |
5,96 |
5,8 |
|
5 |
6,61 |
5,79 |
5,41 |
5,19 |
4,74 |
4,56 |
|
6 |
5,99 |
5,14 |
4,76 |
4,53 |
4,06 |
3,87 |
|
7 |
5,59 |
4,74 |
4,35 |
4,12 |
3,64 |
3,44 |
|
8 |
5,32 |
4,46 |
4,07 |
3,84 |
3,35 |
3,15 |
|
9 |
5,12 |
4,26 |
3,86 |
3,63 |
3,14 |
2,93 |
|
10 |
4,96 |
4,10 |
3,71 |
3,48 |
2,98 |
2,77 |
|
15 |
4,54 |
3,68 |
3,29 |
3,06 |
2,54 |
2,33 |
|
20 |
4,35 |
3,49 |
3,1 |
2,87 |
2,35 |
2,12 |
А) для 
|
|
1 |
2 |
3 |
4 |
10 |
20 |
|
1 |
4052 |
4999 |
5403 |
5,625 |
6036 |
6209 |
|
2 |
98,5 |
99 |
99,17 |
99,25 |
99,4 |
99,45 |
|
3 |
34,12 |
30,82 |
29,46 |
28,71 |
27,23 |
26,69 |
|
4 |
21,2 |
18 |
16,69 |
15,58 |
14,55 |
14,09 |
|
5 |
16,26 |
13,27 |
12,06 |
11,91 |
10,05 |
9,55 |
|
6 |
13,74 |
10,92 |
9,78 |
9,15 |
7,87 |
7,39 |
|
12 |
9,33 |
6,93 |
5,95 |
5,41 |
4,30 |
3,86 |
|
17 |
8,4 |
6,11 |
5,18 |
4,67 |
3,59 |
3,16 |
|
20 |
8,1 |
5,85 |
4,94 |
4,43 |
3,37 |
2,94 |
|
30 |
7,56 |
5,39 |
4,51 |
4,02 |
2,98 |
2,55 |
|
40 |
7,31 |
5,18 |
4,31 |
3,83 |
2,8 |
2,37 |
|
100 |
6,9 |
4,82 |
3,98 |
3,51 |
2,5 |
2,06 |
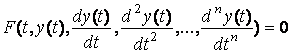